手游《无尽的拉格朗日》与数学中的拉格朗日理论、奇美拉概念的奇妙关联
在现代的手游市场中,一个新的名字正逐渐引起公众的注意:《无尽的拉格朗日》。作为一款带有科幻色彩的策略手游,它不仅仅提供了精致的视觉效果和丰富的游戏内容,更有意思的是,它的名称和部分设计灵感与数学中的拉格朗日理论以及神话生物奇美拉之间存在诸多意想不到的联系。在本文中,我们将解锁这些令人好奇的关系,一探究竟。
数学和物理中的拉格朗日点(Lagrange Points)是天体力学中的一种概念,由意大利数学家约瑟夫-路易·拉格朗日提出。在两个大质量天体(例如地球和月亮)的共同引力场中,存在五个特殊的点,小质量物体可以相对于这两大质量天体保持相对静止的位置。这五个点被称为L1到L5,是天体力学中动态稳定的重要示例。
在《无尽的拉格朗日》中,游戏设计师可能借用了拉格朗日点这一概念,将其转化为游戏世界中的重要节点,玩家可以在这些节点展开战术争夺,保持势力平衡,甚至作为跳跃点挑战新的空间领域。如此一来,游戏在保留了科学根基的也增加了战略层次和空间想象的丰富性。
在数学的另一个分支中,拉格朗日也提出了拉格朗日插值法。这是一种用多项式在给定的几个点上插值的方法。简单来说,拉格朗日插值能够让我们通过少量已知的点,构建一条完整的曲线或函数图像。
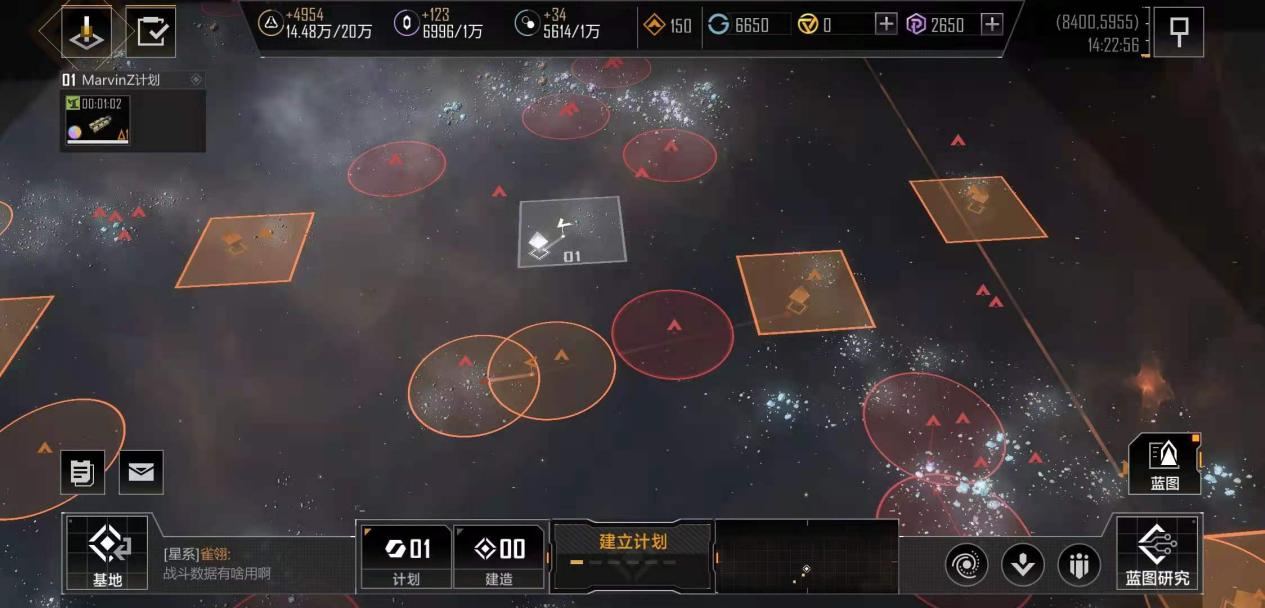
《无尽的拉格朗日》的游戏构建或许从这一数学概念中汲取了灵感,玩家根据限定的资源和条件,创造出个人的游戏战略路径,这类似于在有限的数据点中寻找最佳曲线。每一次决策和部署都像是在进行拉格朗日插值,通过最优化的路径推进游戏进程。
奇美拉在希腊神话中是一种具有狮头、羊身和蛇尾的怪物,代表了混合与不可能。这个名称在后世被用来描述由不同物种组成的混合生物或有多种特性的事物。
在《无尽的拉格朗日》中,“拉格朗日奇美拉”可能是对一种拥有多重属性或功能的游戏元素的称呼。游戏中的某型飞船或装备可能融合了不同文明的科技,既符合科幻设定,又与奇美拉的混合特性相呼应。毫无疑问,设定中这种混合性质的元素会为玩家的体验增添许多趣味。
这种融合概念在游戏设计上表现为不同种族、科技和战术的结合使用,让玩家在策略上有了更多的自由度和创造性。通过对奇美拉的引用,《无尽的拉格朗日》展现了其在多种元素混合上的独特设计思路,并将拉格朗日的数学理念具体化为游戏世界中的一种复杂而多元的体验。
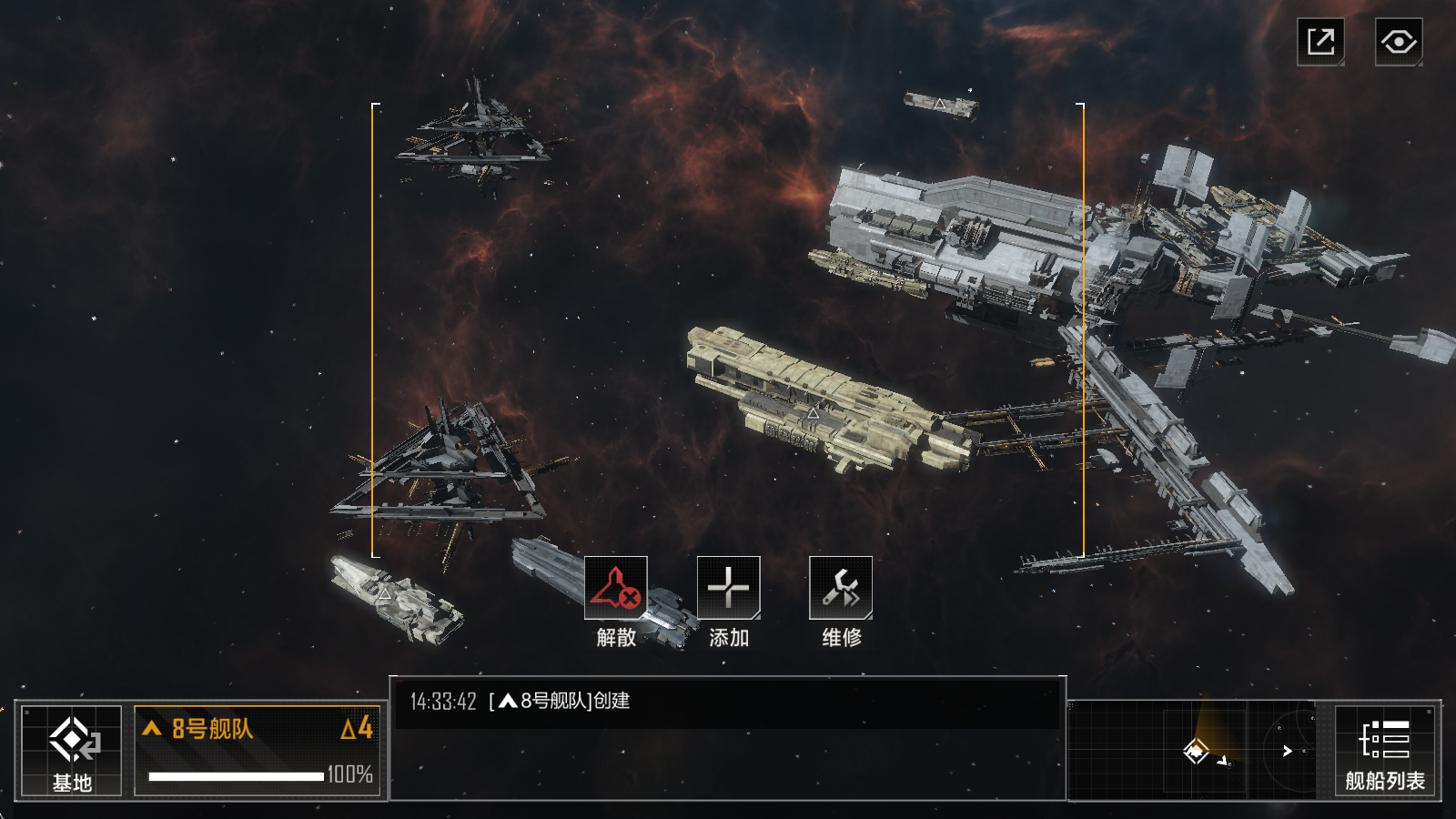
在表面的数字和模型之下,数学是对宇宙原理的深层探讨。游戏《无尽的拉格朗日》不仅让玩家感受到数学概念的神秘和美感,更让他们在游戏的虚拟世界里亲自体验这些概念。游戏场景的设定、战斗系统的规则、以及策略制定的过程,无不体现出数学原理的影响。
《无尽的拉格朗日》的精髓或许就在于此,它将数学的抽象概念和科幻的想象力结合在一起,为玩家创造了一个无限发散的思考和探索空间。通过游戏的桥梁,玩家可以以一种全新且互动的方式来触碰数学和科学思想。

《无尽的拉格朗日》是一个将复杂数学概念与游戏设计巧妙融合的例证。游戏中的拉格朗日点和奇美拉元素不只是一些随意的名词,它们在宏观上富含天体物理和数学的内涵,同时在微观上呈现出游戏设计中对科幻与策略的巧妙结合。数学原理的普遍性以及科幻元素的无限想象空间,使得这款游戏不仅仅是一个消遣品,更是一座桥梁,连结着科学的真理和人类的创造力。
通过这种方式,《无尽的拉格朗日》向我们展示了一个事实:无论是在科学研究中还是在文化娱乐产品中,数学都能够展示它的力量和美丽。在未来,我们期待有更多的作品能够借鉴这种方式,将科学与艺术、数学与游戏、知识与娱乐紧密地结合起来,让我们在探索和乐趣中获得成长和灵感。